Introduction
La blockchain et les réseaux distribués plus généralement sont réputés pour leur transparence et leur immuabilité.
Ces deux qualités sont le fruit d’algorithmes complexes et de technologie telles que les arbres de Merkle leur permettant de produire des preuves pour l’ensemble des transactions et données présentes sur le réseau.
Dans cet article, nous nous attarderons particulièrement sur les Preuves de Merkle ou Merkle Proof en anglais qui rendent tout ceci possible.
Rappel
Les arbres de Merkle (Merkle trees)
Avant toute chose, il est important de faire un léger rappel de ce qu’est un arbre de Merkle.
Pour faire simple, un arbre de Merkle est une structure de donnée basée sur des hashs cryptographiques.
Il est un des composants fondamentaux des réseaux blockchain d’aujourd’hui, car il permet à celle-ci d’être inviolable et immuable.
Un système distribué sans arbre de Merkle impliquerait que chaque nœud (node) du réseau doive enregistrer chaque transaction qui s’est produite, car il n’y a pas de copie centrale des informations comme sur un réseau centralisé.
Cela signifie une quantité phénoménale d’informations (le grand livre dans son ensemble) détenue par chaque nœud à l’identique. Ainsi si un nœud souhaite vérifier une transaction, l’utilisateur demandera à tous les autres nœuds la copie du grand livre qu’ils détiennent afin de les comparer avec sa propre copie.
Des quantités de données comme celle-ci ne seraient pas concevables pour un réseau distribué sécurisé et efficient.
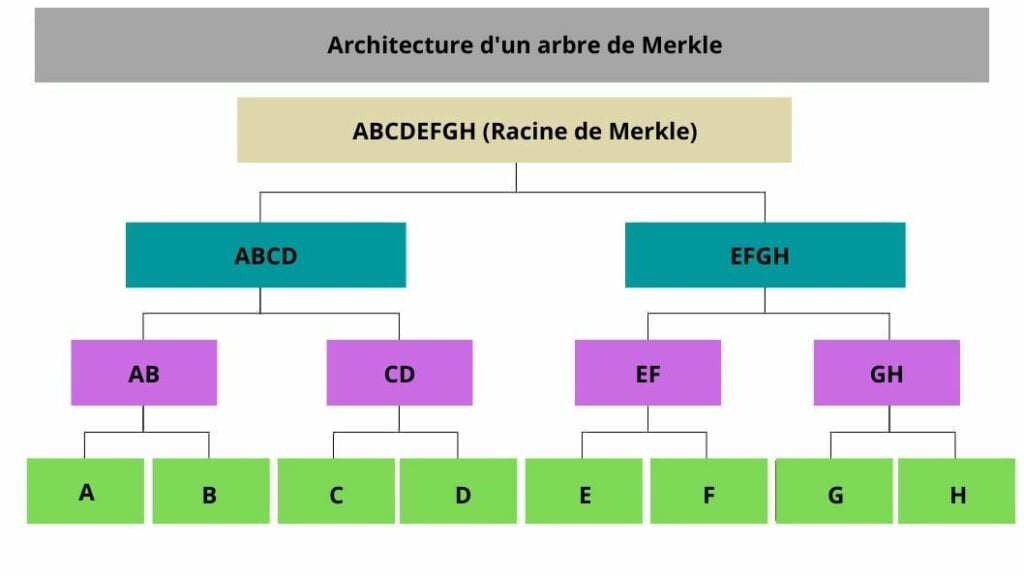
Concrètement, le fonctionnement d’un arbre est relativement simple, on calcule l’empreinte de chaque feuille (données), puis on unit ces empreintes deux par deux afin de calculer un nouveau hash et ceci jusqu’à ce qu’il ne reste qu’une seule empreinte (la racine).
Si vous souhaitez creuser plus en profondeur le sujet, nous avons un article dédié aux arbres de Merkle et leur conception.
Qu’est-ce qu’une Preuve Merkle (Merkles proof) ?
Nous avons brièvement vu au-dessus pourquoi un système distribué ne pourrait pas fonctionner correctement sans les arbres de Merkle.
Les preuves de Merkle sont un des piliers des réseaux informatiques distribués et leur permettent, via un arbre de hashs (Merkle tree), de valider et vérifier les données présentes dans les blocs.
En effet, ces arbres fonctionnent à l’aide de preuve de Merkle permettant de vérifier et confirmer des transactions spécifiques sans avoir à en vérifier la totalité des données.
Vous l’aurez compris, elles permettent d’identifier sans effort des composants spécifiques (données) à une structure de données cryptographiques (Arbre de Merkle).
Les preuves Merkle sont utilisées pour vérifier les facteurs suivants :
- Si les données appartiennent bel et bien à l’arbre de Merkle dont il est question
- Prouver de manière concise la validité de données faisant partie d’un ensemble de données sans stocker l’ensemble des données (comme expliqué précédemment)
- Garantir la validité d’un certain « groupe » de données faisant partie d’un ensemble de données plus vaste sans révéler ni l’ensemble de données complet ni son sous-ensemble
Comment fonctionne une preuve Merkle
Le concept est de hacher de manière répétée différents sous-ensembles de donnée.
Une preuve de Merkle est établie en calculant le hash de chaque paire de nodes. Cette valeur de hachage est propagée au niveau suivant puis le processus est répété en remontant l’arbre jusqu’à arriver au hachage de la racine qui est connu du public ou peut être connue.
En d’autres termes, les racines de Merkle reflètent les hachages combinés d’un bloc de données.
Les modifications supplémentaires apportées aux transactions sont facilement identifiables, car toute altération des hachages des nœuds (feuilles et branches) modifie la racine de hachage.
Étant donné que les hachages à sens unique sont censés être des algorithmes déterministes (purement déterminé par leurs entrées sans facteur aléatoire) et sans collision, deux hashs ne peuvent pas être identiques.
Prenons un exemple pour illustrer ces propos qui peuvent paraitre quelque peu barbares.
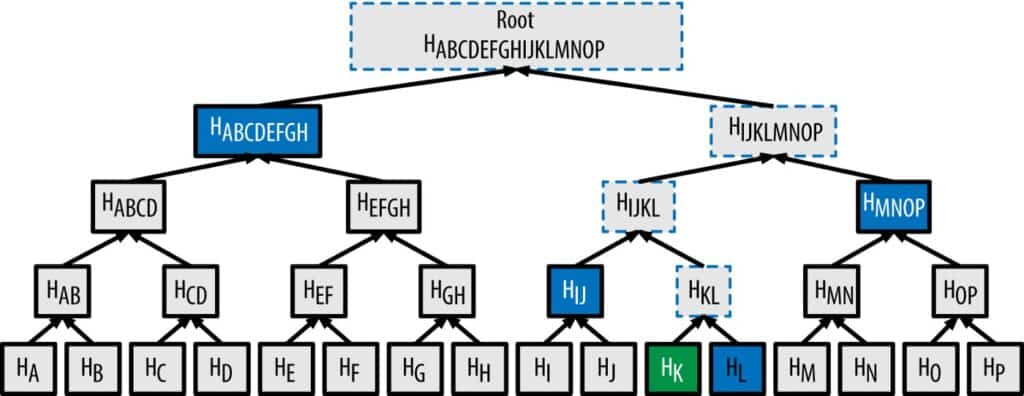
Dans l’exemple ci-dessous, le hash de la racine (merkle root ABCDEFGH) renvoi aux hashs combinés de l’arbre de Merkle représentés par les hachages des feuilles (A, B, C, D, E, F, G, H) et des branches (AB, CD, EF et GH) qui elle-même représente le hash des branches supérieures (ABCD et EFGH).
Les preuves de Merkle permettent ainsi aux nœuds de vérifier chaque donnée de bloc en ne possédant uniquement que le hash racine (hash root ou racine de Merkle).
Dans notre exemple, pour prouver que la transaction C fait bien partie de l’arbre, il faudra calculer le hash de toutes les branches supérieures nécessaire pour arriver à la racine (ABCDEFGH).
Dans notre cas, les hashs nécessaires seront D, AB et EFGH pour la vérification de la transaction C.
Voilà comment fonctionne une preuve de Merkle.
Il est important de noter que pour la vérification de 8 feuilles (A, B, C, D, E, F, G et H dans notre exemple), seulement 3 hashs intermédiaires (D, AB et EFGH dans l’exemple ci-dessus) seront nécessaires, mais qu’il en nécessiterait 19 pour la vérification de 500 000 feuilles (fragments de données).
Ceci montre que plus ce mécanisme est utilisé à grande échelle, plus il devient rentable.
Conclusion
Vous l’aurez compris, les arbres et les preuves de Merkle sont essentiels au bon fonctionnement des systèmes distribués. Ils offrent une économie de données téléchargées non négligeable et permettent une vérification efficace des données.
Ceux-ci sont un concept important à appréhender pour comprendre l’ensemble de la technologie se cachant derrière nos précieux cryptoactifs.